《资本论》第五卷第一部分(十二)
第一章:价值(12)
价值第四定律
这里, 我们请大家看另外一个坐标图:

(图1-3,同一个价值周期中的生命、需求、价值和事物关系图)
这个图中说明了这样几种关系:
首先,在同一个价值周期中,在事物的物理量大于生命的需求量的情况下,当劳动还没有发生的时候,需求和价值在量上是对等的。在上图中,当生命的需求量是6公斤的时候,事物的价值量一定是6公斤。 而当生命的需求量是3公斤的时候,事物的价值量一定是相应的3公斤。需求与价值的数量之间的这种关系,和我们人类照镜子的情况一模一样。在上面这个图里,“生命”轴就好比是镜子,而左边的需求在照镜子,右边的事物的价值,就是镜子中出现的需求的模样。因此,在同一个价值周期中,在事物的最大物理量的范围内,需求和价值的量,永远是同时出现,并且总是相等的。关于这一点,我们在“价值第二定律”中已经说明。
但是,生命的需求,总是需要消耗事物的价值去满足,就是说,当一公斤的价值被消耗掉的时候,原来存在的一公斤的需求同时被抵消了。这说明,等量的需求和价值,在坐标中的方向一定是相反的,这样他们才能相互抵消。而我们上面图1-2中已经说明了,价值的量最小值为零,不存在负数。那么,毫无疑问地,根据需求和价值的镜像关系,则需求就只能是负方向的,并且它的最大值只可能是0,否则它就会在正方向上与价值相遇,而失去相互之间的镜像性。
因此,通过上图, 我们可以更完善地叙述价值的第二定律了:
“价值的第二定律”的完整内容:
在同一个价值周期中,在一个事物所具有的物理量能实现的价值量的最大限度内:1)事物的价值量,和生命对它的需求量相等。简单说,即:对事物的需求量,就是事物的价值量。
2)在同一个量度单位下,一个事物所能具有的价值量的最大量,等同于它自身所具有的相同度量单位的物理量的最大量。
3)当生命对事物的需求量大于事物本身具有的最大物理量时,事物所能具有的最大价值量只能与事物本身的最大物理量相等,不会再随需求的增加而增大。
4)生命对事物的需求量与事物的价值量是,并且只能是,同时等量存在,而正负方向相反。需求量的最大值为0,价值量的最小值为0。表现它们之间关系的正确的计算公式是:Rn+Vn=0 (Rn<或=Mn).
对“价值的第二定律”中的第四点,有四种不同的坐标表示方法。其中之一是图1-3:需求线段与价值线段以生命轴为中心线成镜像。另外三个分别是:
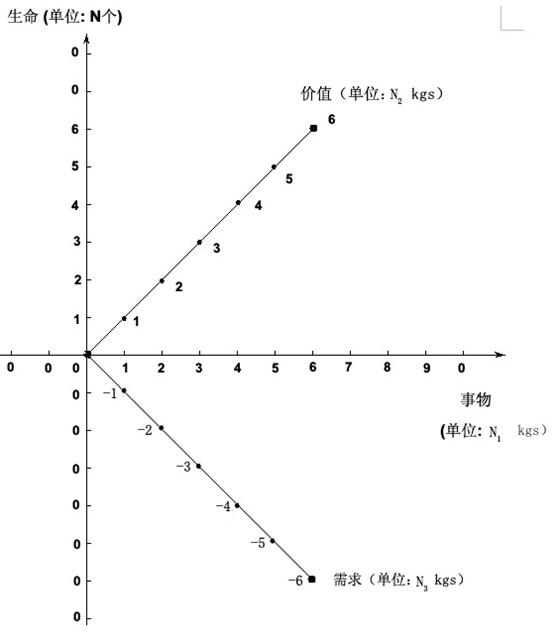
(图1-4:需求线段与价值线段以“事物”轴为中心线成镜像)
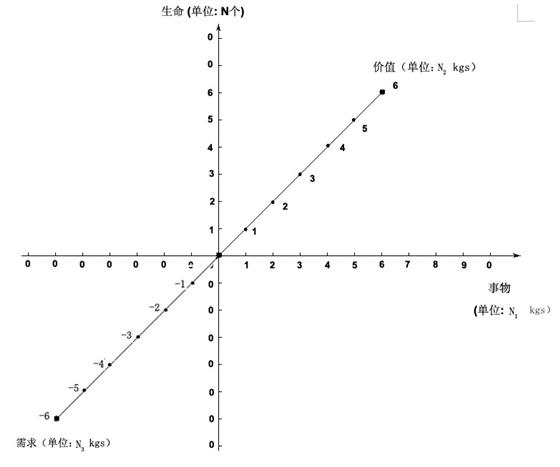
(图1-5:需求线段与价值线段以0点为中心成镜像)

(图1-6:需求线段与价值线段以0点为中心成镜像)
图1-6,与图1-5是同一个图。由于在图1-5中,需求与价值以0圆点为中心成镜像,不再需要“生命”线或“事物”线做参照,因此可以略去,由此得出图1-6的图像。在这个图中, 线段OV是价值线段,线段RO是需求线段。线段ROV则构成了价值周期中的需求-价值状态线。
图1-6是一个非常有用的图。根据“价值的第二定律”中的第四点,我们知道,RO与OV永远是等长的,并永远存在于0圆点的两端。因此,线段RV就表现出一个很有趣的特性:它好象一只乌龟的两只前爪,伸长则两边同时伸长,而缩短则两边同时缩短,最短的时候,是RO和OV两边同时为零。另外,这条ROV线段还可以单独地取出来,放到另外的任何一个我们想将它放进去的坐标中。这给我们使用它来研究市场中的供求关系提供了一个非常好的工具。
这里, 我们大家就通过一些实例来看一下如何使用这个ROV线段。
我们举一个例子。
在不考虑二手市场的情况下,我们将29寸液晶电视在广州市一年内的市场销售设定为一个价值周期。我们假设,这个周期里的需求量是24万台,我们将ROV线段作X轴,而将29寸液晶电视按时间段划分的市场投放量作Y轴,建立起一个图:
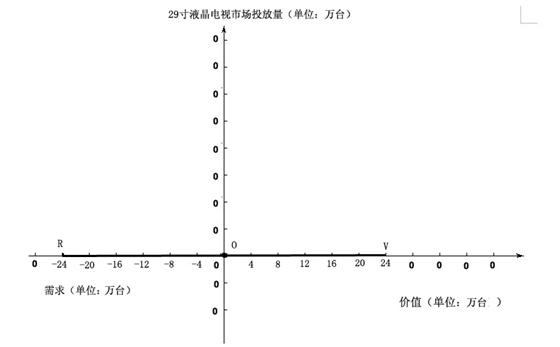
(图1-7,广州市一年内29寸液晶电视供求关系的初始状态图)
这个图我们命名为(假定)“广州市一年内29寸液晶电视供求关系的初始状态图”。在这个图中,需求和价值的量都处在我们假设的最大量的位置。它说明,在这个状态下,市场中还没有29寸液晶电视。因此市场处于商品0投入的初始状态。我们将这一点总结为:
在需求存在而商品还没有投入的市场中,该类商品的价值总值处于最大值状态。
我们假设, 每2个月,广州市的29寸液晶电视的投放量为5万台。并在一年之内有6次投入。然后,我们把每次投入以后的ROV线段在图中描出来,就得到下面的图1-8:
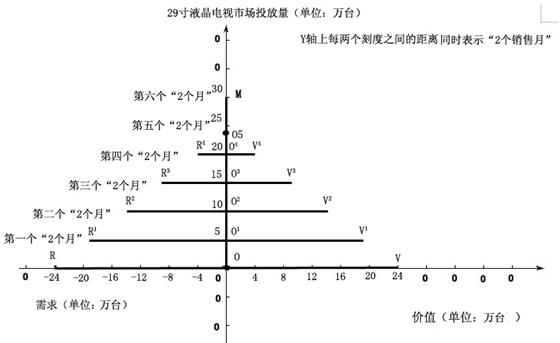
(图1-8,ROV金字塔模型)
于是,以时间为方向,以商品投入线段为中轴,通过上图,我们看到,商品零投入的时候,需求量或价值量(RO或OV值)最大,为24万台。首2个月,当商品投入量为5万台以后,需求量或价值量(RO或OV值)下降到19万台。
为什么“当商品投入量为5万台以后,需求量或价值量(RO或OV值)下降到19万台”呢?这一点,从我们前面几节中对价值的定义和分析中可以得到解释:它是说,商品是“事物”,而我们消耗事物,事实上是消耗事物的价值去满足需求。因此,我们投入5万台电视时,我们同时消耗了5万台电视的价值,并且也同时满足了5万台电视的需求。因此价值OV的长度减少5万。而需求的值RO也同比减少5万。于是我们有了ROV¹线段。并根据相同的道理产生出ROV²、ROV³等等。
当OM线段发展到O-O5时,商品的总投入量已经达到24万,市场达到饱和状态,RO和OV都成为0,因此ROV此时与圆点O5重合。
同时,我们还留意到,在O-O5之后,还继续有商品投入,因为O-O5才进行到第9.6个月,这一年还剩下2.4个月,还有6万台商品会继续投入市场,于是我们有了O5-M线段.可是,由于市场需求RO和市场价值OV现在已经为0,所以,尽管后续有6万台商品投入,可它们的价值已经为0。(在后面关于劳动和货币的章节中,我们会继续分析到,消费者买商品,买的是它的价值量,而不是它的物理量。)这样,由于这6万台商品的价值量为0,它们进入市场之后就不会再有销售,所以只能充当货架上的摆设。
ROV金字塔模型是一个很有意思的图。它说明:由于需求量和事物的价值量是形成价值周期的前提,即:首先必须形成一定量的需求和价值,才可能形成价值周期,因此,在一个特定的价值周期中,需求量和事物的价值量一定是定量的。那么,在需求和价值定量的前提下,事物实现的价值量越大,则它剩下的需求量就越小。反之,如果事物价值实现的量越小,那么生命对它的需求的量就越大。当事物实现的价值量与需求量相等的时候,这个价值周期中该事物的需求量和价值量同时为零,这时,这个价值周期就结束了。在该价值周期之后,无论还剩下有多少物理量的事物,相对于这个已经结束的价值周期而言,它们的价值量都为零。
我们将这个特性总结为:
在一个特定的价值周期中:
第一,总需求量随着实现的总价值量的增加而减少。简单说,即:需求随着价值的实现而递减。我们称之为“需求的递减规律”。
第二,当事物实现的价值量与需求量相等的时候,这个价值周期中该事物的需求量和价值量同时为零,这时,价值周期结束。在价值周期之后,无论该事物还剩下多少物理量,在本价值周期中,它们的价值量为零。
我们将这两点命名为“价值第四定律”,也可以叫作“ROV金字塔定律”。
200810130223初稿
200912202350第一次修改
