友情提示:本博文为原创,已在2014海峡两岸周易学术论坛暨第25届周易与现代化国际讨论会上公开发表,并已获得版权登记,谢绝转载与刊登。如有意向请事先联系,刊登本博文章一律请支付稿费,否则保留追究法律责任的权利。
内容提要:本文深刻阐述了目前很少使用的被称之为半正矢函数(三角函数之一)的太极因子概念,研究分析了该函数表征的太极系统所具有的周期变化、对立统一、阴阳消长、阴阳转化、阴阳极化、阴阳单调变化等特性,引入数学运算方法将太极系统内部的阴阳因子相互和合、差和、交合作用关系简化为和、差、积的数学表现形式。运算结果表明,阴阳因子相互作用除了能够让太极系统展现实物与波的物理现象之外,更具有重大意义的是作者还发现其交合作用会产生一个新太极系统的阴阳因子,用现代科学的方法演绎并证实了太极阴阳理论所揭示的阴阳生生不息、万物繁衍不止的自然哲学原理。太极图实质上是太极因子及其相互作用的完美诠释。
关 键 词:三角函数、太极因子、太极阴阳理论、太极因子的特性、太极因子的作用、太极图
一、太极因子概念
在《太极图的数学模型探讨》一文中作者引入了太极因子的概念。太极因子是从月相发光和阴暗面积的求解过程中发现的,详见于《月相的太极图演变规律探讨》。我们通常能够观察的月相可以用象视面积的变化过程来诠释,月相的明暗圆缺现象可以用数学形式表达。众所周知,月相是最常见的周而复始、循环往复的变化现象,其内部具有太极阴阳演变规律。因此,我们把数学表达式中能够反映太极演变规律的函数称之为太极因子。
在互联网上经百度搜索,原来太极因子是三角函数的一种形式——半正矢函数,数学表达为:
半正矢函数 haversinθ=(1-cosθ)/2
havercosinθ=(1+cosθ)/2
公元5世纪时印度最早在引入正弦概念的同时也引入了正矢函数,记载于《苏利耶历数书》(约400年)中。三角函数包含六种基本函数:正弦函数、余弦函数、正切函数、余切函数、正割函数、余割函数。与正矢函数相同形式的是一组罕见的三角函数。
正矢函数 versinθ=1-cosθ
vercosinθ=1+cosθ
余矢函数 coversinθ=1-sinθ
covercosinθ=1+sinθ
半正矢函数 haversinθ=(1-cosθ)/2
havercosinθ=(1+cosθ)/2
半余矢函数 hacoversinθ=(1-sinθ)/2
hacovercosinθ=(1+sinθ)/2
外正割函数 exsecθ=secθ-1
外余割函数 excscθ=cscθ-1
半正矢函数就是这些现在很少使用的三角函数之一。在探讨中国古代传统文化的过程中,我们发现半正矢函数具有独特的性质,能够全面完整系统地表述太极阴阳理论。因此,我们给这一组三角函数赋予全新的概念——太极因子。
太极是一个整体系统,是阴阳合和体。太极系统可由阴和阳两个特性组成,阴和阳是太极处于两仪层次的表现形式,阴的特性用字符Y- 表示,阳的特性用字符Y+ 表示。用阴、阳特性构建的太极理论称之为太极阴阳理论或阴阳太极理论。
与太极阴阳理论相对应的是,当太极系统处于高度有序的稳定状态时,两仪层次的阴阳特性同样可以用阴阳因子表征。阴因子能够表达太极系统中阴的特性,用字符Y-表示,阳因子能够表达太极系统中阳的特性,阳因子用字符Y+表示。阴阳因子的数学表达式为
Y- =(1-cosθ)/2 (1)
Y+ =(1+cosθ)/2 (2)
那么,阴阳因子是如何表达太极系统中阴阳特性的呢?它们又是如何在太极系统中产生作用的呢?下面我们就这些问题对阴阳因子这一组函数所蕴含的特性以及它们之间产生的作用进行讨论。
二、太极因子的内在特性
太极系统的内在特性就是阴阳因子的内在关系。有关阴阳之间的内在关系,我们的前人已经作过大量的研究分析,大致可归纳为周期变化特性、对立统一特性、阴阳消长、转化特性、阴阳极化特性、阴阳单调特性等等。
1. 周期变化特性
阴阳因子是三角函数的一种特殊形式,根据三角函数的性质,阴阳因子是一组周期性函数。周期性函数是指随时间的变化不断出现重复的现象。两个重复现象所需的最短时间称之为周期。在用相(视)角表示的函数中,两个重复现象所需的最小角度称之为周角。通常周期函数的周角为2π弧度即360度,也就是观察者经过一周的观察其观察结果会出现重复。
对于周期变化的函数,可以用数学表达式表示:
Y(θ+2Kл) = Y (θ) (3)
式中: θ为观察事物变化的角度,2Kл为太极系统的周期,K为自然数即太极系统的周期数。
阴阳因子用观察角θ表示为
Y- (θ) = (1-cosθ)/2
Y+ (θ) = (1+cosθ)/2
当观察角为θ+2Kл时,阴阳因子表示为
Y- (θ+2Kл)= (1-cos(θ+2Kл))/2 = (1-cosθ)/2
Y+ (θ+2Kл)= (1+cos(θ+2Kл))/2 = (1+cosθ)/2
所以有:
Y- (θ+2Kл) = Y- (θ) (4)
Y+ (θ+2Kл) = Y+ (θ) (5)
(4)(5)表明阴阳因子是周期性函数,用阴阳因子表征的太极系统是一个周期性变化系统。
2. 阴阳对立特性
反映事物状态的太极系统都可以用阴、阳两个特性来表示。太极系统的阴阳特性,是观察者从同一方向或同一角度对同一系统状态获得的两个特性相反的观察结果。所谓相反就是对立,在观察角度上成π弧度或180度。换句话说,就是观察者在某一方向上对系统状态进行观察,观察的结果为阳,那么,观察者转过或绕过180度后对系统状态进行观察,观察的结果为阴。如果观察的结果为阴,那么,转过或绕过180度后观察的结果则为阳。
设开始的观察角度为θ,与此相反的观察角度为θ±л,可对阴阳因子(1)(2)作如下变换:
Y- (θ±л) = (1-cos(θ±л))/2 = (1+cosθ)/2
Y+ (θ±л) = (1+cos(θ±л))/2 = (1-cosθ)/2
所以有:
Y- (θ±л) = Y+ (θ) (6)
Y+ (θ±л) = Y- (θ) (7)
(6)(7)表明阴阳因子是一组相互对立的函数,用阴阳因子表征的太极系统的阴与阳具有相互对立特性。
3. 阴阳统一特性
太极系统由阴和阳两个特性组成,是阴阳的合和体。如果太极系统用字符H表示,根据定义,太极系统可用数学表达式表示为
H = Y+ + Y- (8)
用(1)(2)代入(8),可得
H = (1+cosθ)/2 + (1-cosθ)/2 = 1
所以有
H = 1 (9)
(9)表明阴阳因子组成了一个完整的太极系统,用阴阳因子表征的阴与阳具有相互统一特性。
4. 阴阳消长、转化特性
由于系统在不断运动,反映系统状态特性的阴与阳也在不断地变化。依据太极系统阴阳统一特性,无论系统如何变化,对系统状态观察的结果都应满足关系式(8)。当系统整体处在平衡稳定状态时,系统的和为恒定不变即H =常量。所以系统的阴阳可以用数学表达式表示为:
Y- = H - Y+ (10)
Y+ = H - Y- (11)
(10)(11)表明一个稳定的太极系统,其内部的阴阳变化遵循一定的规律,即系统的阴增加时阳就会减少,反之,当系统的阴减少时阳就会增加。用(1)(2)和(9)代入(10)(11),可得
Y- = H - Y+ = 1-(1+cosθ)/2 = (1-cosθ)/2
Y+ = H - Y- = 1-(1-cosθ)/2 = (1+cosθ)/2
阴因子可以由阳因子转化得到,阳因子可以由阴因子转化得到,这就是太极系统的阴阳消长、转化特性。
5. 阴阳极化特性
由于阴阳因子是一组周期性变化函数,而且在一定区间内变动,变化区间为[0,1],所以,阴阳因子具有极点现象。阴阳因子具有极大值和极小值。当阴因子为最小值0时,阳因子为最大值1,太极系统只表现出阳的特性,系统处于阳极状态。反之,当阳因子为最小值0时,阴因子为最大值1,太极系统只表现出阴的特性,系统处于阴极状态。因为系统是变化的,根据系统的阴阳相互转化特性,我们把经过极点的阴阳相互转化称之为阴阳极化。当太极系统处于阳极状态时的变化为阳极阴返,反之,当太极系统处于阴极状态时的变化为阴极阳返。这就是太极系统的阴阳极化特性。
6. 阴阳单调特性
由于阴阳因子是一组周期性变化函数,只要分析一个周期的变化情况就可以清楚所有可能的状态。在一个周期内,阴阳因子的变化可按观察角θ分为两个区间,区间[0,π]和区间(π,2π]。在区间[0,π]内,阴因子为单调增函数,阳因子为单调减函数。在区间(π,2π]内,阴因子为单调减函数,阳因子为单调增函数。阴阳因子的单调特性如表1所示。
表1 太极因子的单调特性
|
观察角
|
θ= 0
|
θ=π/2
|
θ=π
|
θ=3π/2
|
θ=2π
|
|
(1-cosθ)/2
|
0
|
0.5
|
1
|
0.5
|
0
|
|
单调特性
|
极小
|
↗
|
极大
|
↘
|
极小
|
|
(1+cosθ)/2
|
1
|
0.5
|
0
|
0.5
|
1
|
|
单调特性
|
极大
|
↘
|
极小
|
↗
|
极大
|
由此可见,我们在分析探讨太极系统的过程当中都是从阴阳的变化特性出发的,即从阴阳的单调变化上考虑的。
从阴阳因子单调增方向研究太极系统时,可选用如下数学表达式
Y- =(1-cosθ)/2 θ∈[0,π] (12)
Y+ =(1+cosθ)/2 θ∈(π,2π] (13)
从阴阳因子单调减方向研究太极系统时,可选用如下数学表达式
Y+ =(1+cosθ)/2 θ∈[0,π] (14)
Y- =(1-cosθ)/2 θ∈(π,2π] (15)
运用阴阳单调特性研究太极系统是太极图理论的基础,从太极图形的分析中可以得出太极图中央的S形曲线实际上都是按照阴阳递增或递减特性绘制的。
三、太极因子的相互作用
太极系统由阴和阳两个主要特性组成。阴和阳两个特性同时存在于系统中,阴与阳就会相互产生作用。除了观察者最直观地观察到太极系统的阴阳合和状态外,系统中的阴阳还会表现出其它各种性质。按阴阳作用的方式可分为:和合作用、差合作用、交合作用。
1. 阴阳和合作用
阴阳和合作用是指太极系统内阴阳两个因子的相互叠加现象。阴和阳两个特性组成了一个整体系统,是阴阳统一特性的表现。因此,阴阳相互叠加的结果产生阴阳和合体:
H = Y+ + Y- (16)
当系统处于稳定的平衡状态时,用(1)(2)代入上式,可得
H = (1+cosθ)/2 + (1-cosθ)/2 = 1
简单概括为
H = 1 (17)
上式说明,当我们用阴和阳两个特性同时观察一个稳定的平衡系统时,观察的结果是一个真实存在的物体,即实物。而且,阴阳具有相互转化特性,阴能转阳,阳能转阴,阴阳之和保持着恒定不变,实物也始终存在。
2. 阴阳差合作用
阴阳差合作用是指太极系统内阴阳两个因子的相互分离现象。与相互叠加现象不同的是,阴阳两个因子的相互分离现象是不能被观察者直接观察的,是隐性的过程状态。阴阳相互分离作用的结果产生阴阳差合体:
H = Y+ - Y- (18)
H = Y- - Y+ (19)
当系统处于稳定的平衡状态时,用(1)(2)代入上式,可得
H = (1+cosθ)/2 - (1-cosθ)/2 = cosθ
H = (1-cosθ)/2 - (1+cosθ)/2 = - cosθ
简单概括为
H = cosθ (20)
H = - cosθ (21)
这是一组余弦函数,在物理上表现出波的特征。
3. 阴阳交合作用
阴阳交合作用是指太极系统内阴阳两个因子的相互交感现象。相互交感作用的结果为
H = Y+ • Y- (22)
当系统处于稳定的平衡状态时,用(1)(2)代入上式,可得
H =((1+cosθ)/2)•((1-cosθ)/2)
H =(1- cos2θ)/4
H =(sin2θ)/4 (23)
上式中有一个三角函数
Y = sin2θ
它可以转换为
Y =(1-cos2θ)/2
设φ=2θ,则上式为
Y =(1-cosφ)/2 (24)
按照太极系统的概念,(24)式表示的是一个以φ为观察角的与原系统不同的太极系统的阴因子。为了与原太极系统相区分,新的太极系统的阴因子表示为
YY- =(1-cosφ)/2 (25)
我们把(22)(23)(25)组合一起,可得
Y+ • Y- =( YY- )/4 (26)
Y- 与YY-具有一个相同的结构形式,这是一个出乎意料的结果。一个太极系统的阴阳因子其交合作用会产生另一太极系统的阴因子或阳因子。这一结果,深刻阐明了太极阴阳理论的阴阳生生不息、万物繁衍不止的自然哲学原理。
四、太极因子的几何图形
表征太极系统函数的主要参数之一是观察角度,因此用极坐标表现太极阴阳理论比较便利。而太极系统函数又以描述观察系统状态的结果为目的,所以采用雷达坐标系更能体现观察结果。雷达坐标系由极点和垂直向上的极轴组成,坐标系中的质点可以用极径和顺时针方向为正的极角表示。太极坐标系则采用雷达坐标系中阴阳因子的组合方式即半周期图形。用太极坐标系绘制的图形当0~π之间表现为阳因子时则π~2π之间表现为阴因子。反之,当0~π之间表现为阴因子时则π~2π之间表现为阳因子。为了便于分析研究,我们用雷达坐标系绘制的图形称之为雷达图,用太极坐标系绘制的图形称之为太极图。按照太极图的绘制方法,一组阴阳因子将会出现两种情况,看起来一种按顺时针旋转,另一种为逆时针。下列图形分析中,省略了逆时针方向变化的图形。
1. 阴阳因子图形
图一是用阴因子(1-cosθ)/2、阳因子(1+cosθ)/2绘制的两个独立的雷达图。
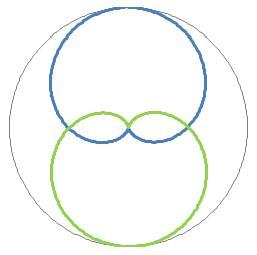

图一 阴阳因子的雷达图 图二 阴阳因子的太极图
图二是用阴因子(1-cosθ)/2、阳因子(1+cosθ)/2绘制的阴阳因子组合的太极图。
太极图与雷达图的主要区别在于:雷达图是阴因子或阳因子全周期的图形,即观察角在0~2π之间的图形,太极图则是半个周期的组合图形,即观察角在0~π和π~2π之间的阳因子和阴因子的组合图形。
2. 阴阳因子和合体、差合体图形
按照阴阳和合作用其结果为H = Y+ + Y- = 1 ,所以阴阳和合体的雷达图和太极图都是以1 个单位为半径的圆,如图三、图四中的外圆所示。
阴阳差合作用其结果为H = Y+ - Y- = cosθ或H = Y- - Y+ = -cosθ,阴阳差合体的雷达图是上下两个半径为0.5个单位的偏心圆,如图三所示。
阴阳差合体雷达图与阴阳因子雷达图是有差异的。除了曲线形状不同外两个系统的观察角度是有区别的。对于阴阳和合体雷达图来说因为其值为H = 1,绘制的图形与系统观察角度无关,而阴阳差合体雷达图有两种结果,H = cosθ和H = -cosθ,分别绘制出相互对称的偏心圆,而且按系统观察角在一个周期内分别画了两圈(相互重叠)。
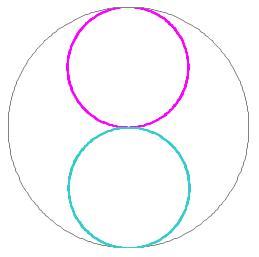
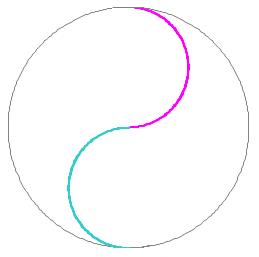
图三 阴阳和合体、差合体雷达图 图四 阴阳和合体、差合体太极图
图四则是阴阳差合体cosθ和-cosθ的太极图,由两个半圆组合而成。同样阴阳差合体太极图与阴阳因子太极图也有差异。除了曲线形状有些不同外,阴阳差合体太极图是用观察角在0~π/2和π~3π/2之间或π/2~π和3π/2~2π之间的两种差合体的组合图形。
3. 阴阳因子交合体图形
图五中间是阴阳交合体雷达图,因为H =(sin2θ)/4 =((1-cosφ)/2)/4,所以图形的幅值为(1-cosφ)/2阴因子的四分之一。而(1-cosφ)/2则是一个以φ为观察角的新系统的阴因子,(1-cosφ)/2阴因子的幅值仍然以1 个单位考虑。故H =(sin2θ)/4 =((1-cosφ)/2)/4的图形幅值为0.25个单位。
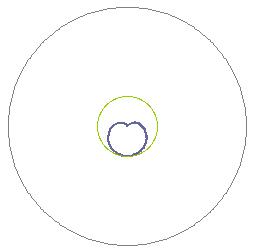
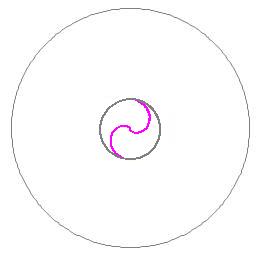
图五 阴阳交合体雷达图 图六 新系统阴阳因子的太极图
与新系统的阴因子(1-cosφ)/2相对应的是,原系统也有可能交合产生新系统的阳因子(1+cosφ)/2。新系统的阴阳因子组成一个新的阴阳因子太极图,如图六中央图形所示。
新系统的阴阳因子同样会产生相互和合作用、差和作用,作用的结果形成一个以0.25个单位的和合体,还有两个以0.125个单位的差和体,如图七所示。
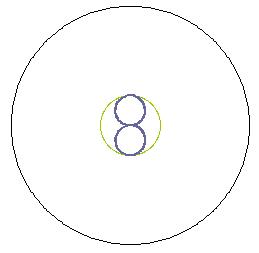
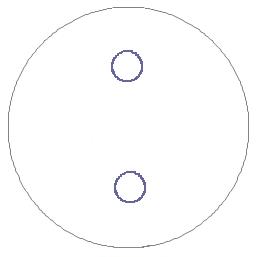
图七 新系统阴阳和合、差合体雷达图 图八 新系统差合体雷达图
由于新系统的差合体有两种状态,而且两种状态分别是以阳因子和阴因子为主导因素时产生的,是两种具有独立性质的状态,因此,可以将两种状态分别绘制在原系统阴阳差合体的中心位置,如图八所示。
如果太极系统内部是一个不断发生相互作用的系统,则系统内各种作用的结果可能会同时存在。当原系统的和合体、差合体与新系统的差合体同时存在时,可以将图八与图四同时绘制在一个图形中,这个图形就是传统的太极图图形,如图九所示。如果用黑白两种颜色分别表标识阴阳两个状态,整个图形也就形成了阴阳双鱼太极图。
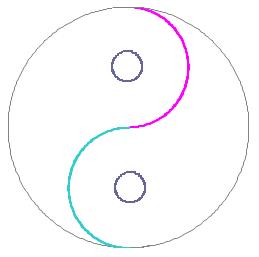

图九 太极图 图十 传统的太极图
由此可见,传统的太极图反映的是新老两个系统阴阳因子相互作用的结果。阴阳鱼为原系统的阴阳差合体,阴阳鱼眼则为新系统的阴阳差合体。它们反映出一个整体的两个不同层次。
需要说明的是为什么原系统的差合体图形是半圆而新系统的差合体图形是整圆。这是因为新老太极系统是两个独立的系统,除了系统的变化幅度不同外,其系统的观察角度也不同,新系统的差合体的幅度是原系统的四分之一,而新系统的观察周角则是原系统的二倍,所以在同一坐标系中,原系统为半周的图形(两个四分之一周),新系统则为一周。
当新系统的阴阳差合体聚集在中间位置时就形成了新系统的阴阳差合体太极图,如图十一所示。
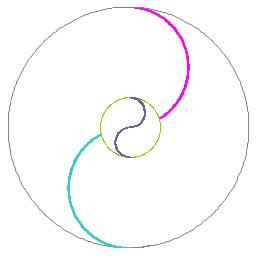
图十一 循环作用的太极图
该图反映出一个太极系统其内部不断相互作用可以产生一个新的太极系统,真实描绘了太极阴阳理论的阴阳生生不息、万物繁衍不止的自然哲学原理。阴阳作用生生不息、循环不止,这就是太极阴阳理论的全部精华所在。
五、结束语
本文深刻阐述了目前很少使用的被称之为半正矢函数(三角函数之一)的太极因子概念,研究分析了该函数表征的太极系统所具有的周期变化、对立统一、阴阳消长、阴阳转化、阴阳极化、阴阳单调变化等特性,引入数学运算方法将太极系统内部的阴阳因子相互和合、差和、交合作用关系简化为和、差、积的数学表现形式。运算结果表明,阴阳因子相互作用除了能够让太极系统展现实物与波的物理现象之外,更具有重大意义的是作者还发现其交合作用会产生一个新太极系统的阴阳因子,因而用现代科学的方法演绎并证实了太极阴阳理论所揭示的阴阳生生不息、万物繁衍不止的自然哲学原理。太极图实质上是太极因子及其相互作用的完美诠释。
参考文献:
1.《太极图的数学模型探讨》《邵雍诞辰1000周年国际学术研讨会会议学术论文集》第96页至104页北京三式乾坤信息技术研究院2011年11月编印
2.《月相的太极图演变规律探讨》《第14回世界易经大会暨第22届周易与现代化国际讨论会论文集》2011年9月出版
3.《太极坐标系》《邵雍诞辰1000周年国际学术研讨会会议学术论文集》第105页至110页北京三式乾坤信息技术研究院2011年11月编印
4.《数学4》(普通高中课程标准实验教科书 必修A版)人民教育出版社等编著并出版2007年2月第2版2009年7月浙江第7次印刷
