基尼系数的EXCEL模拟计算
熊义杰
(西安理工大学 经济与管理学院 710054)
摘要:国内不少学者曾对基尼系数的具体计算方法作了探索,提出了多个不同的计算公式。本文笔者利用EXCEL通过拟合回归曲线,运用EXCEL中的函数功能,提出了一种通过计算定积分和模拟计算基尼系数的方法,很值得推广使用。
关键词:基尼系数;EXCEL;模拟计算
基尼系数是国际社会用来考察收入分配平等程度的一个指标,该指标的大小直接反映了一个国家收入分配的状况,也在某种程度上反映了一个国家社会的稳定性程度。
1. 什么是基尼系数
基尼系数,是20世纪初意大利经济学家基尼根据洛伦茨曲线所定义的判断收入分配公平程度的指标,其比例数值在0和1之间,是国际上用来综合考察居民内部收入分配差异状况的一个重要分析指标。
系数值的计算是设实际收入分配曲线和收入分配绝对平等曲线之间的面积为A,实际收入分配曲线右下方的面积为B。并以A除以(A+B)的商表示不平等程度,如图1所示。这个数值被称为基尼系数或称洛伦茨系数。如果A为零,基尼系数为零,表示收入分配完全平等;如果B为零则系数为1,收入分配绝对不平等。收入分配越是趋向平等,洛伦茨曲线的弧度越小,基尼系数也越小,反之,收入分配越是趋向不平等,洛伦茨曲线的弧度越大,那么基尼系数也越大。基尼系数计算的一般公式是:
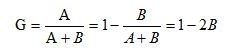 (1)
(1)
公式很容易理解,因为A+B的面积等于0.5,也就是1/2。国内不少学者曾对基尼系数的具体计算方法作了探索,提出了多个不同的计算公式。其中,一个简便易用的公式是,假定一定数量的人口按收入由低到高的顺序排队,分为人数相等的n组,从第1组到第i组人口累计收入占全部人口总收入的比重为wi,然后利用下面的公式计算基尼系数。不难看出,该公式是利用定积分的定义将洛伦茨曲线的积分(面积B)分成n个等高梯形的面积之和得到的。
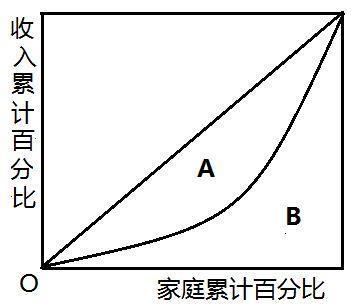
图1
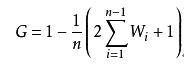
日本学者使用的公式是:
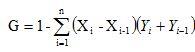
其中,Xi是累计的家庭比率,Yi是累计的收入比率[1]。
这两个公式的意义其实是一样的。因为将横轴分成n等份后,每个等份就是1/n,而Xi-Xi-1也就是1/n,这就是小梯形的高,Yi=Wi即小梯形的下底。我们知道,梯形的面积就等于上底加下底乘高除2,除2与公式(1)中的乘2相约,上底加下底时每个下底会被加2次(第一个是个小三角形),最后的一个小梯形的下底是1,只加一次。因此,实际应用中也可以用下面的公式计算:
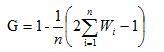 (2)
(2)
基尼系数的具体含义是指,在全部居民收入中,用于进行不平均分配的那部分收入所占的比例。基尼系数最大为“1”,最小等于“0”。前者表示居民之间的收入分配绝对不平均,即100%的收入被一个单位的人全部占有了;而后者则表示居民之间的收入分配绝对平均,即人与人之间收入完全平等,没有任何差异。但这两种情况只是在理论上的绝对化形式,在实际生活中一般不会出现。因此,基尼系数的实际数值只能介于0~1之间,基尼系数越小收入分配越平均,基尼系数越大收入分配越不平均。国际上通常把0.4作为贫富差距的警戒线,大于这一数值容易出现社会动荡。
联合国有关组织规定:若低于0.2表示收入绝对平均;0.2~0.3表示比较平均;0.3~0.4表示相对合理;0.4~0.5表示收入差距较大;0.5以上表示收入差距悬殊。
基尼指数一般以0.4作为收入分配差距的“警戒线”,根据黄金分割律,其准确值应为0.382。一般发达国家的基尼指数在0.24到0.36之间,美国偏高,为0.45。全球基尼系数最高的地方是非洲的纳米比亚,亚洲地区的中国大陆和香港的基尼系数都超过0.4。2001年以后,香港甚至达到0.525,2006年更高达0.533,成为发达国家及地区中,贫富悬殊最严重的地区;即使把发展中国家包括在内,香港也在全球贫富差距最严重程度中名列前茅,仅次于萨尔瓦多、哥伦比亚、洪都拉斯、智利、危地马拉、巴拿马、巴西、津巴布韦、南非、巴拉圭、玻利维亚、海地、中非共和国、塞拉利昂、博茨瓦纳、莱索托、纳米比亚而排名倒数18位。
在国际社会,日本是全球基尼系数最低的国家之一。据共同社2013年10月11日报道,日本厚生劳动省公布的2011年调查报告显示,日本国内基尼系数为0.2708,创历史新高。据报道,自1984年以来,日本的基尼系数持续上升,此次调查较2008年的数据增加0.0218,创历史新高。厚劳省认为,收入较低的老年人及单身者家庭的增加导致差距扩大。在日本,基尼系数的调查每三年左右实施一次,此次是第16次。日本的基尼系数一般在0.25左右,德国为0.3左右,而美国的基尼系数已经超过0.4的警戒线。发展中国家基尼系数一般较高,大致在0.4上下。日本基尼系数较低的一个重要原因是政府通过实行高额累进税制“劫富济贫”,高收入群体的最高所得税税率达到75%,一般低收入群体只有15%。美国普通中产阶级的税率大致为15%或25%,比较富有的中产阶级可能要支付35%。但由于超级富豪的投资收入适用的税率不超过15%,比工资收入应缴的税率低不少,因此很多富翁的收入适用的税率远低于一般中产阶级。
在薪酬制度设计上注重薪酬保障作用的日本,薪酬收入差距较小;而注重激励作用的美国,薪酬收入差距往往达数十倍甚至上百倍。其结果是美国经济与社会具有较强的活力和创新能力,但社会的割裂和碎片化明显;而日本社会则较为稳定,即使发生如1998年那样的大危机也未产生重大的社会问题,但社会活力和创新能力又略显不足。
中国国家统计局基尼公布基尼系数2014年为0.469,2013年为0.473,2012年为0.474,2010年为0.481。根据西南财经大学教授甘犁主持,西南财经大学中国家庭金融调研中心发布统计报告称2010年为0.61,已跨入收入差距悬殊行列,财富分配非常不均。但这个数据存在争论,被很多业内学者质疑。学者岳希明和李实在《华尔街日报》撰文称甘犁主持的报告称其统计样本过小和住户收入所需信息上存在问题,所以统计值过大。甘犁随后在2013年1月24日在《华尔街日报》撰文回应相应问题。2013年2月5日岳希明和李实再次在《华尔街日报》发表文章,认为甘犁的回应没有很好地回答大部分的质疑,他们对西南财经大学公开的项目数据进行再次计算,进行再质疑。国家发改委社会发展研究所所长杨宜勇认为,西财的基尼系数更像是银行金融资产的基尼系数,而不是收入的基尼系数。又北京大学中国家庭动态跟踪调查显示2012年中国基尼系数为0.49。北京大学中国社会科学调查中心发布《中国民生发展报告2014》。该报告称,中国的财产不平等程度在迅速升高:1995年我国财产的基尼系数为0.45,2002年为0.55,2012年我国家庭净财产的基尼系数达到0.73,顶端1%的家庭占有全国三分之一以上的财产,底端25%的家庭拥有的财产总量仅在1%左右。
基尼系数除了用以反映居民收入分配的均衡性外,还可以用以考察一个国家经济发展的均衡性。比如,用一个国家不同地区(省或洲)国土面积的累计百分比做横轴,以这些不同地区所生产的GDP的累计百分比做纵轴,即可一个国家经济发展的均衡性。
以上事实说明,基尼系数的测算十分重要。国际社会为基尼系数设置警戒线本身就表明,对于基尼系数必须引起高度警惕,否则将会引发一系列社会问题,进而造成社会动荡,甚至会危及到社会主义的国家政权。
2. 基尼系数的模拟计算
在这里,我们要讨论的是如何利用EXCEL来计算模拟基尼系数。
首先,第一步,需要先对数据进行整理。据有关资料,美国4个不同年份中5个不同等级家庭的收入比重如表5-1所示。
表5-1 美国4个不同年份5个不同等级家庭收入比重
|
收入等级 |
1966年 |
1980年 |
1990年 |
2005年 |
|
第一等级 |
5.6 |
5.3 |
4.6 |
4 |
|
第二等级 |
12.4 |
11.6 |
10.7 |
9.6 |
|
第三等级 |
17.7 |
17.6 |
16.6 |
15.3 |
|
第四等级 |
23.8 |
24.4 |
23.8 |
23 |
|
第五等级 |
40.5 |
41.1 |
44.3 |
48.1 |
|
合 计 |
100 |
100 |
100 |
100 |
对5个不同等级的家庭收入进行累计,整理后不同等级的家庭累计的收入比重数据如表5-2所示。
表5-2 美国4个不同年份5个不同等级家庭收入累计比重
|
收入等级 |
累计家庭 比率(X) |
累 计 收 入 比 率 (Y) |
|||
|
1966年 |
1980年 |
1990年 |
2005年 |
||
|
第一等级 |
0.2 |
0.056 |
0.053 |
0.046 |
0.04 |
|
第二等级 |
0.4 |
0.18 |
0.169 |
0.153 |
0.136 |
|
第三等级 |
0.6 |
0.357 |
0.345 |
0.319 |
0.289 |
|
第四等级 |
0.8 |
0.595 |
0.589 |
0.557 |
0.519 |
|
第五等级 |
1 |
1 |
1 |
1 |
1 |
有了表5-2,第二步,就可以利用累计家庭比率(X)和各年累计的收入比率(Y)在EXCEL上绘制散点图,拟合洛伦茨曲线了。方法是:
1)先在EXCEL上输入变量X和Y的数值;
2)选中数据;
3)在常用工具栏上打开“图表向导”;
4)选定“XY散点图”,进入下一步;
5)完成散点图的有关选项(包括标题、网格线、图例、数据标志等)
有了散点图,就可以在散点图上插入趋势线,构造回归方程了。回归方程通常的参考形式是“二次曲线”(不带常数项)或“乘幂函数”。 “插入趋势线”的方法是:
1)点击散点图中任一数据点使数据点变亮,再右键单击;
2)在对话框中选择“添加趋势线”命令;
3)在“类型”标签中选“多项式(P)”(阶数(D)=2)或“乘幂(W)”型。
4)在“选项”标签中选“显示公式”和“显示R平方值”(对于多项式需另选“设置截距=0”)。
究竟选哪一个曲线函数,以两个曲线函数所得到的“R平方值”的大小决定,选“R平方值”大的。因为“R平方值”的大小放映了回归的曲线对样本数据揭示的百分比,“R平方值”越大,对样本数据揭示的百分比就越大。根据经验,“乘幂函数”的“R平方值”更大,所以一般选“乘幂函数”更好。
接下来,第三步,就可以估计和模拟基尼系数了。这里可以有三种方法供选择使用。
方法一,我称之为公式法,是直接使用公式(2)进行计算。对美国4个不同年份的基尼系数利用公式(2)计算的结果是:
G1966=0.3248,G1980=0.3376,G1990=0.37,G2005=0.4064。
方法二,我称之为积分法,即求所构造的回归曲线在(0,1)区间的定积分。乘幂函数的一般形式是 aXb,其原函数是aXb+1/(b+1),当X取0值的时候其值为0,当X取1的时候其值就是a/(b+1),这也就是公式(1)中B的面积。因此,利用公式(1)即可直接算出基尼系数。
美国4个不同年份构造的乘幂型回归曲线分别为:
![]()
4个函数的“R平方值”分别为:0.9975,0.9969,0.9955,0.9928;均比2阶多项式函数的“R平方值”要高。
由这些回归函数即通过积分法计算的美国4个不同年份的基尼系数分别为:
G1966=0.3321,G1980=0.3464,G1990=0.3792,G2005=0.4167。
与公式法的计算结果比较,均略大,差值在2~3%之间。
方法三,就是我们这里要重点讨论的“模拟法”,这种方法即通过模拟计算定积分的值得到所需结果。下面以美国1966年的数据为例予以说明。
第一步,先利用函数“=RAND()”生成两个随机数,前者为X,后者为Y。
第二步,利用函数“=IF(B31<0.9221*C31^1.7612,1,0)”考察Y是否落在曲线之下。
最后利用函数“=COUNTIF(D31:D5030,"=1")”统计线下次数(假定模拟了5000次),计算基尼系数,基尼系数利用公式“G=1-B/(A+B)”计算,其中(A+B)=2500,即模拟实验次数的一半,B就是统计的线下次数。
对于其它3个年份的模拟,无需另外生成随机数,只消在另外的列用当年的曲线函数代替上述第二步中的曲线函数即可。比如,1980年为“=IF(B31<=0.9146*C31^1.7985,1,0)”,1990年为“=IF(B31<=0.8931*C31^1.8771,1,0)”,2005年为“=IF(B31 <=0.86091* C31^ 1.9518,1,0)”。
对模拟的结果进行误差分析,通过多次模拟后发现,误差的大致区间为-3%~8%,正误差较大,负误差较小,这与构造的回归函数有关。因为由回归函数的定积分计算的基尼系数均为正误差,误差在2~3%之间。
参考文献
1. 【日】白沙堤津耶 著 瞿 强 译 《通过例题学习计量经济学》,北京:中国人民大学出版社,2012(2)
2. 张建华 《一种简便易用的基尼系数计算方法》,山西农业大学学报(社会科学版) 2007年第6卷(第3期)
